Flavours of homotopy theory

Roy Magen (ICMS, IMI-BAS)

Резюме: In this talk we will consider different flavours of homotopy theory for different types of geometric contexts. First we will recall the usual definitions of the homotopy category, and equivariant homotopy categories, and we will show how we can think of these in terms of (equivariant) smooth manifolds. This will give us a suitable framework with which to adapt the notion of homotopy theory to different geometries.
We first use this framework to give a brief overview of the story in algebraic geometry, which produces motivic homotopy theory. Next, we will use our framework to discuss notions of homotopy theories parametrized by a geometric object, and discuss some consequences.
Depending on time constraints and interest, we will end either by discussing work relating this homotopical framework to 6-functor formalisms, by going over a version of this story in the complex analytic setting, or by introducing C∞-schemes and discussing possibilities for an extension of the story for manifolds to this setting.

Distinguished non-Kähler metrics on compact complex manifolds

Liviu Ornea (University of Bucarest)

Резюме:   I shall review the definitions of LCK, pluriclosed and balanced metrics and discuss their incompatibility on the same compact complex manifold.

Concircularly Semi-Symmetric Metric Connection

Miroslav Maksimović, Университет на Прищина в Косовска Митровица, Косовска Митровица, Сърбия, и Институт по математика и информатика, Българска академия на науките

Резюме. A concircularly semi-symmetric metric connection is a special class of semi-symmetric metric connection when its generator is a concircular vector. In this talk, we will present results on this connection on pseudo-Riemannian manifolds, and in particular, we will observe the application to Lorentzian manifolds and the theory of relativity. We demonstrate that a Lorentzian manifold reduces to a GRW space-time when the generator of the observed connection is a unit timelike vector. At the same time, the mentioned connection becomes a semi-symmetric metric P-connection. At the end, we determine the equation of state on a perfect fluid space-time. These are the results of a joint work with prof. Milan Zlatanović published in J. Geom. Phys. 217 (2025).

The lecturer is supported by the Scientific Programme “Enhancing the Research Capacity in Mathematical Sciences (PIKOM)”, No. DO1-67/05.05.2022.

Hodge-Riemann balanced structures on non-Kähler manifolds

Asia Mainenti, IMI and ICMS, Sofia

Резюме:  A Hodge-Riemann balanced structure on a complex manifold is the datum of a balanced metric whose (n-1)-th power can be decomposed into the wedge product of two differential forms, satisfying the classical Hodge-Riemann bilinear relations. Such structures were introduced by X. Chen and R. Wentworth, to generalize the nonabelian Hodge correspondence to non-Kähler Hermitian metrics. However, there are no known examples of Hodge-Riemann balanced structures on non-Kähler manifolds. The aim of this talk is to address this lack of examples, highlighting the relation with p-Kähler structures and discuss some obstruction results in the class of solvmanifolds. Lastly, we will present the first example of such a structure on a non-Kähler, non-compact complex manifold obtained as the product of the Iwasawa manifold by C. This is joint work with A. Fino.

Special metrics in hypercomplex geometry

Elia Fusi, University of Torino

Резюме: The existence of special hyperHermitian metrics plays an important role in the study of hypercomplex manifolds. In this talk, after a brief overview of the basic definitions in hypercomplex Geometry, we will discuss two of the main types of special metrics in the hypercomplex setting: quaternionic Gauduchon and strong HKT metrics. First of all, we will discuss sufficient and equivalent conditions for a quaternionic Gauduchon metric to exist.  Afterwards, we will show that strong HKT and balanced hyperHermitian metrics cannot coexist on a compact non-hyperKähler manifold, proving a particular instance of the Fino-Vezzoni conjecture. Finally, we will introduce an Einstein condition for hyperHermitian metrics and describe the similarities with the Kähler-Einstein case.

This is a joint work with Giovanni Gentili.

Weak Metric Structures on Generalized Riemannian Manifolds

Milan Zlatanovic, University of Niš, Serbia

Резюме. Linear connections with torsion are important in the study of generalized Riemannian manifolds (M, G=g+F), where the symmetric part g of G is a non-degenerate (0,2)-tensor and F is the skew-symmetric part. Some space-time models in theoretical physics are based on (M,G=g+F), where F is defined using a complex structure. In the lecture, we will show more general models, where F has constant rank and is based on weak metric structures (introduced by the V. Rovenski and R. Wolak), which generalize almost contact and f-contact structures. We consider metric connections (i.e., preserving G) with totally skew-symmetric torsion tensor. For rank(F)=dimM and non-conformal tensor A2, where A is a skew-symmetric (1,1)-tensor adjoint to F, we apply weak almost Hermitian structures to fundamental results (by S. Ivanov and M. Zlatanovic) on generalized Riemannian manifolds and prove that the manifold is a weighted product of several nearly Kahler manifolds corresponding to eigen-distributions of A2. For rank(F)<dimM we apply weak f-structures and obtain splitting results for generalized Riemannian manifolds.
(This is joint work with Vladimir Rovenski, Department of Mathematics, University of Haifa).

Посещението на лектора е финансирано по Научна програма “Повишаване на изследователския капацитет в областта на математическите науки (ПИКОМ)”, № ДО1-67/05.05.2022.

Higher order estimates for Monge-Ampere type equations motivated by quaternionic geometry

Marcin Sroka, Jagiellonian University, Kraków, Poland

Резюме. In the talk I will discuss obstacles for obtaining higher order a priori estimates for equation introduced by Alesker and Verbitsky in 2010 on HKT manifolds in relation to Calabi type conjecture on those manifolds (and similar type PDEs studied since on hypercomplex manifolds). After presenting the state of art, I will focus on the key second order estimate. For the real Monge-Ampere equation on Riemannian manifolds it follows essentially by Pogorelov calculation, for the complex Monge-Ampere equation, in relation to Calabi conjecture, it was proven by Aubin and Yau. I will use those two as comparison to underline new difficulties related to concavity properties of quaternionic Monge-Ampere operator.

Посещението на лектора е финансирано по Научна програма ” Повишаване на изследователския капацитет в областта на математическите науки (ПИКОМ)”, № ДО1-67/05.05.2022.

Unimodality Preservation by Ratios of Functional Series and Integral Transforms

Dmitrii Karp, Holon Institute of Technology, Holon, Israel

Резюме: Elementary, but very useful lemma due to Biernacki and Krzyz (1955) asserts that the ratio of two power series inherits monotonicity from that of the sequence of ratios of their corresponding coefficients. Over the last two decades it has been realized that, under some additional assumptions, similar claims hold for more general series ratios and integral transforms as well as for unimodality in place of monotonicity. In the talk, we discuss conditions on the functional sequence and the kernel of an integral transform ensuring such property. Numerous series and integral transforms appearing in applications satisfy our sufficient conditions, including Dirichlet, factorial and inverse factorial series, Laplace, Mellin and generalized Stieltjes transforms, among many others. The key role in our considerations is played by the notion of sign regularity.

Презентация

Complex Dirac structures on flag manifolds

Carlos Augusto Bassani Varea, Universidade Tecnológica Federal do Paraná, Brazil

Резюме. In this talk we present a description of the invariant complex Dirac structures with constant real index on a maximal flag manifold in terms of the roots of the Lie algebra which defines the flag manifold. As a particular case, when the real index is zero, we have the description of all invariant generalized complex structures on a maximal flag manifold. We also present a classification of the complex Dirac structures under the action of B-transformation. This is a joint work with Cristian Ortiz (IME-USP).

New and little known properties of the Fox and Fox-Wright functions

Dmitrii Karp,
Holon Institute of Technology, Holon, Israel

Резюме. In the talk, I will introduce the functions H of Fox and W of Wright (its general case known as Fox-Wright function) and some motivation behind them. Then, I will discuss the extension of Gauss’ expansion and summation formulas for the hypergeometric function to the case of general Fox-Wright function and Norlund’s expansion for the Meijer’s G function to the case of Fox’s H function. I will further present positivity conditions for the so-called delta-neutral case of Fox’s H function making it a probability distribution (widely used in statistics), which rely on complete monotonicity of certain product ratios of Gamma functions. Moreover, I will exhibit a new integral equation for Fox’s H function and a conjecture regarding its zeros. Finally, some open problems will be presented.

Burau Representation and Application to Reducibility and Exchangeability of Braids

Alexander Stоimenov,
Dongguk University, Republic of Korea

Резюме. I will give an introduction to the braid groups, closure operation, Markov theorem, and exchange move. Then I will introduce the Burau representation, and discuss its application to reducibiliy and exchangeability of braids.

Independence Structures in Random Matrix Theory and Random Partitions

Yacine Barhoumi-Andréani,
University of Bochum, Germany

Резюме. We consider two models of random objects: eigenvalues of random matrices and random integer partitions for two classical measures: the GUE and the Schur measure. We express the largest element of these sets as maxima of independent random variables. The method uses orthogonal polynomials on the real line in the random matrix case and on the unit circle in the second case. The distribution involved in the random matrix case uses the sigma-form of Painlevé IV functions whose theory will be recalled.

Функции холоморфни над крайно-мерни комплексни комутативни алгебри

Марин Генов,
Институт по математика и информатика – БАН

Резюме. Всеки морфизъм φ: A → B в категорията на крайно-мерните комплексни комутативни асоциативни унитални (Банахови) алгебри поражда структурен сноп от функции на една A-променлива и със стойности в B, чийто диференциал е съвместим с A-модулната структура на B. Оказва се, че макар и това да са изображения на няколко комплексни променливи, те притежават и много свойства на функциите на една комплексна променлива. Същевременно това дава възможност за изграждането на относителен комплексен анализ и относителна (на ниво скалари и в смисъла на Гротендик) комплексно-аналитична геометрия. В доклада ще разгледаме някои основни аспекти и въпроси на локалната аналитична теория.

Riemannian four-manifolds and twistor spaces: some rigidity results

Davide Dameno,
Department of Mathematics “Federigo Enriques”, University of Milan

Резюме. It is well-known that four-dimensional Riemannian manifolds carry many peculiar properties, which give rise to the existence of unique canonical metrics. In order to find conditions for the existence of such metrics, in 1978 Atiyah, Hitchin and Singer adapted Penrose’s construction of twistor spaces to the Riemannian context, paving the way for the study of many other characterizations of curvature properties for Riemannian four-manifolds. After giving an overview of the Riemannian and Hermitian structures of twistor spaces in the four-dimensional case, we present some new rigidity results for Riemannian four-manifolds whose twistor spaces satisfy specific vanishing conditions (such as Bochner-flatness). This is based on joint work with Professors Giovanni Catino and Paolo Mastrolia.

Въведение в спектрална теория на графите, част 3

Петър Петров,
Институт по математика и информатика – БАН

Резюме. Тази лекция съдържа спектрален подход към визуализацията и дзета функции на Ихара за прости графи. Както и преди, ударението ще бъде върху възможни приложения и формалните доказателства ще бъдат изложени накратко или въобще пропуснати. Ще се предполагат съвсем базисни познания по линейна алгебра и аналитични функции.

Въведение в спектрална теория на графите, част 2

Петър Петров,
Институт по математика и информатика – БАН

Резюме. Втората лекция включва още някои основни понятия, като матрица на инцидентност и дуален граф. Графичното представяне на граф и разделяне на кластери ще бъдат обсъдени също. Докато в първата лекция целта беше мотивацията, в тази лекция ще наблегнем на теореми и примери.

Въведение в спектрална теория на графите

Петър Петров,
Институт по математика и информатика – БАН

Резюме. Това е първата лекция от цикъл от 2-3 лекции по алгебрична теория на графите. Тя ще е достъпна за слушатели с минимални знания по линейна алгебра, в това число за специалисти по информатика или биостатистика, както и за студенти. Примери ще демонстрират всяко понятие. Всичко необходимо от теория на графите ще бъде дадено. Упорът е главно върху приложения. Ще бъде разгледан Лапласиана на граф и някои негови свойства, а също за какво може да се използва и как може да се пресмята.

Zener model with General fractional calculus: Thermodynamical Restrictions

Teodor M. Atanackovic and Stevan Pilipovic,
Serbian Academy of Sciences and Arts and University of Novi Sad, Serbia

Резюме. We study a Zener type model of viscoelastic body within the context of general fractional calculus and derive restrictions on coefficients that follow from the dissipation inequality that is, the entropy inequality under isothermal conditions. We show, for a stress relaxation and a wave propagation, that the restrictions that follow from the entropy inequality are sufficient to guarantee the existence and uniqueness of the solution. We present numerical data related to the solution of a wave equation for several values of parameters.

Surfaces Associated with Pascal and Catalan Triangles

Leonard DAUS¹, Marilena JIANU¹ and Adela MIHAI^1,2,
¹ Technical University of Civil Engineering Bucharest, Romania,
² Transilvania University of Brasov, Romania

Резюме. An open problem in reliability theory is that of finding all the coefficients of the reliability polynomial associated with particular networks. Because reliability polynomials can be expressed in Bernstein form (hence linked to binomial coefficients), it is clear that an extension of the classical discrete Pascal’s triangle (comprising all the binomial coefficients) to a continuous version (exhibiting infinitely many values in between the binomial coefficients) might be geometrically helpful and revealing [1]. We investigated in [2] some geometric properties of a continuous extension of Pascal’s triangle: Gauss curvature, mean curvature, geodesics and level curves, as well as their symmetries. As a next step [3], we investigate a surface related to one of the Catalan triangles presented in [4].  

References: 

[1] M. Jianu, L. Daus, M. Nagy, R.M. Beiu, Approximating the level curves on Pascal’s surface, International Journal of Computers, Communications & Control 17(4) (2022), art. 4865. 

[2] V. Beiu, L. Daus, M. Jianu, A. Mihai, I. Mihai, On a surface associated with Pascal’s triangle, Symmetry 14(2) (2022), art. 411. 

[3] M. Jianu, S. Achimescu, L. Daus, I. Mierlus-Mazilu, A. Mihai, D. Tudor, On a surface associated to Catalan triangle, submitted. 

[4] L. Daus, M. Jianu, R.M. Beiu, V. Beiu, A tale of Catalan triangles – counting lattice paths, 9th International Workshop on Soft Computing Applications – SOFA 2020, 27-29 November 2020, Arad, Romania. 

Funding: Work supported by the research project SUPREMA UTCB-CDI-2022-008 of the Technical University of Civil Engineering Bucharest. 

On Squeezing Function for Planar Domains

Ahmed Yekta Ökten, Institut de Mathématiques de Toulouse, France

Резюме. Let Ω be a domain in ℂ^𝑛 such that the set 𝐸(Ω, 𝐵^𝑛) of injective holomorphic maps from Ω into the unit ball 𝐵^𝑛 ⊂ ℂ^𝑛 is non-empty. The squeezing function of Ω, denoted by 𝑆_Ω is defined as

𝑆_Ω(𝑧) = sup{𝑟 ∈ (0, 1): 𝑟𝐵^𝑛 ⊂ 𝑓(Ω),      𝑓 ∈ 𝐸(Ω, 𝐵^𝑛),      𝑓 (𝑧) = 0}.

It follows from the definition that the squeezing function is biholomorphically invariant and roughly speaking, it measures how much a domain looks like the unit ball looking at a fixed point. As expected, the study of the squeezing function leads to nice results about the properties of the invariant metrics on complex domains. The behaviour of the squeezing function is well studied however very few non-trivial explicit formulas of squeezing functions have been found.

In this talk we will establish the explicit formulas of squeezing functions on doubly connected planar domains in an elementary way. With the same method we will also provide bounds to squeezing functions of higher connected domains. Finally, we will conclude by mentioning other results and further questions about explicit formulas of squeezing functions on planar domains.

Въведение в хомологичната огледална симетрия на проективни равнини с тегла над комплексните числа

Марин Генов,
Институт по математика и информатика, БАН

Резюме. Ще въведем основните понятия и резултати водещи до формулировката на хомологичната огледална симетрия в случая на проективните равнини с тегла над комплексните числа.

Севджан Хаккъев,
Шуменски университет

Резюме. В този доклад, ще представим някои резултати, свързани с устойчивостта на периодични вълни. В моделите, които ще разгледаме, проблема за устойчивост се свежда до изследването на  спектрални задачи от вида

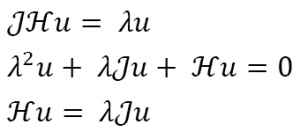
и пресмятането на определени величини, свързани с индекса на устойчивост.

The Dimension Dind оf Finite Topological T0-Spaces

Dimitrios Georgiou,
University of Patras, Greece

Резюме. A.V. Arhangelskii introduced the dimension Dind [2] and some properties of this dimension have been studied in [1, 3]. In this talk, we present the study of this dimension for finite T0-spaces. Especially, we present that in the realm of finite T0-spaces, Dind is less than or equal to the small inductive dimension ind, the large inductive dimension Ind and the covering dimension dim. We also give the “gaps” between Dind and the dimensions ind, Ind and dim, presenting various examples which shows these “gaps”. Moreover, in this field of spaces, we present characterizations of Dind, inserting the meaning of the maximal family of pairwise disjoint open sets, and give properties of this dimension.
References:[1] Chatyrko V.A., Pasynkov B.A., On sum and product theorems for dimension Dind, Houston J. Math. 28 (2002), no. 1, 119-131.[2] Egorov V., Podstavkin Ju., A definition of dimension, (Russian) Dokl. Akad. Nauk SSSR 178 1968, 774-777.[3] Kulpa W., A note on the dimension Dind, Colloq. Math. 24 (1971/72), 181-183.
The results of this talk are the research work of the paper “THE DIMENSION Dind OF FINITE TOPOLOGICAL T0-SPACES”, the authors of which are D. Georgiou, Y. Hattori, A. Megaritis and F. Sereti. This paper has been accepted for publication to the journal Mathematica Slovaca.

Обобщени ротационни повърхнини в 4-мерни псевдо-Евклидови пространства

Виктория Бенчева,
Институт по математика и информатика, БАН

Резюме. Ротационните повърхнини са богат източник на примери както в Евклидови така и в псевдо-Евклидови пространства. В доклада разглеждаме т. нар. обобщени ротационни повърхнини от елиптичен и хиперболичен тип в 4-мерно пространство на Минковски и в 4-мерно псевдо-Евклидово пространство с неутрална метрика, които са аналог на дефинираните от C. Moore обобщени ротационни повърхнини в Евклидовото пространство R4. Oписваме аналитично някои техни подкласове: минимални, плоски, с плоска нормална свързаност, с паралелен нормиран вектор на средната кривина.

Формални околности в пространства от дъги

Алгоритъм на Висковатов за полиноми на Ермит-Паде

Algebraic Non-hyperbolicity of Hyperkähler Manifolds

Людмила Каменова (Stony Brook University, USA)

Резюме. A projective manifold is algebraically hyperbolic if the degree of any curve is bounded from above by its genus times a constant, which is independent from the curve. This is a property which follows from Kobayashi hyperbolicity. We prove that hyperkahler manifolds are not algebraically hyperbolic when the Picard rank is at least 3, or if the Picard rank is 2 and the SYZ conjecture on existence of Lagrangian fibrations is true. We also prove that if the automorphism group of a hyperkahler manifold is infinite, then it is algebraically non-hyperbolic. These results are joint with Misha Verbitsky.